Heterogeneous Front‑Door Effects, Gently Explained

Created on September 26, 2025

2025   ·   causal inference   front-door   heterogeneous treatment effects   debiased ML   orthogonal learning

This is a gentle introduction of our work on estimating heterogeneous Front‑Door Effects.

TL;DR. When unmeasured confounding breaks back‑door adjustment but a mediator is observed and well‑explained by covariates, front‑door adjustment can still identify causal effects. This post introduces two learners—FD‑DR‑Learner and FD‑R‑Learner—that estimate heterogeneous (personalized) front‑door effects. Both achieve quasi‑oracle rates (i.e., as fast as if you knew the true nuisance functions) when nuisances converge as slowly as $n^{-1/4}$-rate (debiasedness). We summarize the ideas, give intuition, show when to use which method, and point you to code.

What “debiased” and “quasi‑oracle” mean here

  • Debiased / orthogonal: the loss functions are constructed so that the first-order sensitivity to nuisance error is zero**. Remaining error enters as products of nuisance errors (e.g., $| \hat m{-}m|\,|\hat q{-}q|$) or higher-order terms.

  • Quasi-oracle rate: An oracle rate is the achievable rate for the target parameter when the true nuisances are given. The quansi-oracle rate is the same as oracle rate from our estimated nuisances.

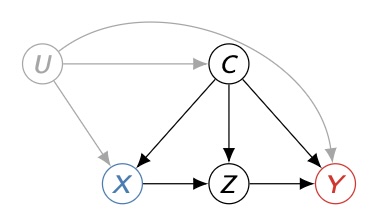
1) Why front‑door HTE?

With observational data, unmeasured confounding often prevents identification of causal effects via the usual back‑door (ignorability) route. Front‑door (FD) adjustment, introduced by Pearl [1], saves the day when a mediator $Z$ carries the effect from treatment $X$ to outcome $Y$, and $Z$ is “sufficiently” explained by observed covariates $C$. Many FD estimators target average treatment effects. However, in practice, we need personalized effects $\tau(C)$ per unit’s baseline characteristics $C$. This work fills that gap with debiased, ML‑friendly HTE estimators under FD.

2) Setup & notation (all symbols defined up front)

  • Observed data: $V=(C,X,Z,Y)$, i.i.d.
    • $C$: covariates (vector).
    • $X\in {0,1}$: binary treatment.
    • $Z\in {0,1}$: binary mediator.
    • $Y$: outcome (real-valued).
    • $U$: unobserved confounders (affecting $C,X,Y$).
  • Nuisance functions (all conditional on $C=c$ unless noted):
    • Outcome regression: $m(z,x,c)\triangleq \mathbb{E}[Y\mid Z=z, X=x, C=c]$.
    • Propensity for treatment: $e(x\mid c)\triangleq \Pr(X=x\mid C=c)$; write $e_1(c)=e(1\mid c)$, $e_0(c)=1-e_1(c)$.
    • Mediator mechanism: $q(z\mid x,c)\triangleq \Pr(Z=z\mid X=x,C=c)$.

  • Target (CATE under FD):

    \[\tau(C)\triangleq \mathbb{E}[Y\mid do(X{=}1),C]-\mathbb{E}[Y\mid do(X{=}0),C].\]

    Under the FD criterion (stated next), this equals

    \[\tau(C)=\sum_{z,x}\big\{q(z\mid 1,C)-q(z\mid 0,C)\big\}e(x\mid C)\,m(z,x,C).\]

    (This is Eq. (4) in the paper.)

  • Front-door criterion (intuitive):

    1. All causal paths $X\to Y$ go through $Z$ (no unmediated direct effect).
    2. Spurious paths $X\leftrightarrow Z$ are blocked by $C$.
    3. Spurious paths $Z\leftrightarrow Y$ are blocked by $(X,C)$.

    Front-door causal diagram

3) Two debiased learners at a glance

We provide two estimators for $\tau(C)$

(1) FD-DR-Learner Builds a pseudo-outcome whose conditional mean equals $\tau(C)$ and regresses it on $C$. It is doubly robust in the FD sense and attains quasi-oracle rates when nuisances have $n^{-1/4}$ rates.

(2) FD-R-Learner Uses a partial linear decomposition of the FD system (two BD-R subproblems for $X\to Z$ and $Z \to Y$), plus a pseudo-g construction to remove first-order dependence on the treatment propensity. Also attains quasi-oracle rates under $n^{-1/4}$ nuisances—without inverse probability ratios, so it is variance-friendly under weak overlap.

4) FD‑DR‑Learner — idea, pseudo‑outcome, and steps

Weights and induced functionals. Define

\[\xi_{\bar x}(Z,X,C)\equiv \frac{q(Z\mid \bar x,C)}{q(Z\mid X,C)},\qquad \pi_{\bar x}(X,C)\equiv \frac{\mathbb{I}\{X=\bar x\}}{e(X\mid C)}.\] \[r_{m,e}(Z,C)\equiv \sum_x m(Z,x,C)e(x\mid C),\quad \nu_{m,e,q}(X,C)\equiv \sum_z r_{m,e}(z,C)q(z\mid X,C),\] \[s^{\bar x}_{m,q}(X,C)\equiv \sum_z m(z,X,C)\,q(z\mid \bar x,C).\]

Front-door pseudo-outcome (FDPO).

\[\phi_{\bar x}(V;\eta)=\xi_{\bar x}\{Y-m\}+\pi_{\bar x}\{r_{m,e}-\nu_{m,e,q}\}+s^{\bar x}_{m,q}.\]

Key property: $\mathbb{E}[\phi_{\bar x}(V;\eta)\mid C]=\mathbb{E}[Y\mid do(X{=}\bar x),C]$, so

\[\mathbb{E}[\phi_1(V;\eta)-\phi_0(V;\eta) \mid C] = \tau(C).\]

Moreover, if either (i) $q$ is right or (ii) $(m,e)$ are right, the construction is unbiased—this is the double-robustness in the FD world (Lemma 2, Thm. 1).

Algorithm (two-way cross-fit).

  1. Split data into $D_1,D_2$.
  2. On $D_1$: fit $\hat m,\hat e,\hat q$.
  3. On $D_2$: compute $\hat\phi_1-\hat\phi_0$ and regress it on $C$ (any ML regressor + regularization) to get $\hat\tau_{DR}(C)$.
  4. Swap folds and average.

Pros/cons. FD-DR is robust to nuisance misspecification and straightforward to implement. It uses inverse weights/density ratios $\pi_{\bar x},\xi_{\bar x}$, which can inflate variance when overlap is weak (propensities near 0 or 1).

5) FD‑R‑Learner — decomposition, pseudo‑g, and steps

Partial linear view of FD. Under the FD criterion the system can be written as

\[\begin{aligned} X&=e_X(C)+\varepsilon_X, \\ Z&=a(C)+X\,b(C)+\varepsilon_Z, \\ Y&=f(X,C)+Z\,g(X,C)+\varepsilon_Y, \end{aligned}\]

with appropriate mean-zero conditions. The heterogeneous effect factorizes as

\[\tau(C)=b(C)\,\gamma_g(C),\qquad \text{ where } \quad \gamma_g(C)\triangleq \mathbb{E}[g(X,C)\mid C].\]

Estimating $b$ and $g$ via BD-R.

  • Treat $(Z,X,C)$ as an R-learner setup to learn $b(C)$.
  • Treat $(Y,Z,(X,C))$ as an R-learner setup to learn $g(X,C)$.
    Each inherits quasi-oracle rates even if nuisances (e.g., $e_X,m_Z,e_Z,m_Y$) only achieve $n^{-1/4}$ (standard BD-R guarantees).

The pseudo-g trick. A naive plug-in for $\gamma_g(C)$ depends linearly on the error in $e_X$. Instead define

\[\zeta(X,C)=\big(1-\tilde e_X(C)\big)\tilde g(0,C)+\tilde e_X(C)\tilde g(1,C) +\{X-\tilde e_X(C)\}\{\tilde g(1,C)-\tilde g(0,C)\}.\]

Then $\mathbb{E}[\zeta\mid C]=\gamma_g(C)$, and its error does not have a first-order dependence on $\tilde e_X$; it only depends on the quality of $\tilde g$ (Lemma 3). Regress $\zeta$ on $C$ to get $\hat\gamma(C)$. Finally, set $\hat\tau_R(C)=\hat b(C)\hat\gamma(C)$. (Def. 5, Thm. 3.)

Algorithm (three-way cross-fit).

  1. Split into $D_1,D_2,D_3$.
  2. On $D_1$: fit nuisances $e_X,m_Z,e_Z,m_Y$.
  3. On $D_2$: run BD-R to learn $\hat b(C)$ and $\hat g(X,C)$.
  4. On $D_3$: build $\hat\zeta$ and regress on $C$ to get $\hat\gamma(C)$.
  5. Output $\hat\tau_R(C)=\hat b(C)\hat\gamma(C)$.
  6. Swap folds and average.

Pros/cons. FD-R avoids density ratios (good under weak overlap) and yields interpretable pathway components $\hat b,\hat g$. It requires more nuisance fits than FD-DR. See §4.1.

6) Snippets on Main Result

The main theorems show that both FD-DR and FD-R learners are debiased estimators. Their error does not depend linearly on errors in nuisance estimates (like $m,e,q$). Instead, nuisance errors only appear in products (e.g., $|\hat m-m|\,|\hat q-q|$), which vanish faster. As a result, as long as each nuisance is learned at the standard $n^{-1/4}$ rate, the estimator of $\tau(C)$ converges at the same rate as if you had the true nuisances in hand. This is called the quasi-oracle property.

On top of that, Theorem 1 shows that FD-DR is doubly robust: it remains unbiased if either the mediator model $q$ is correct or the pair $(m,e)$ is correct.

Theorems 2 and 3 establish the guarantees for FD-R: it avoids density ratios entirely, making it more stable when overlap is weak, while still attaining quasi-oracle rates. In short, the theory says FD-DR is safer when you trust one nuisance strongly, while FD-R is safer when propensities are extreme and variance control matters most.

7) Which learner should I use?

  • Use FD-DR-Learner when you can accurately estimate either $q(Z\mid X,C)$ or the pair $(m,e)$, and overlap is decent. You’ll benefit from double robustness.

  • Use FD-R-Learner when overlap is weak (propensities near 0/1), you want variance stability (no density ratios), or you value interpretability via $\hat b(C)$ and $\hat g(X,C)$ for diagnostics.

This mirrors the analytical comparison in §4.1 and the patterns in Fig. 2.

8) Practical checklist

  1. Positivity/overlap diagnostics. Check empirical support of $e(X\mid C)$ and $q(Z\mid X,C)$; consider ratio stabilization/weight clipping (on denominators only) and overlap-aware uncertainty. (See discussion & limitations.)

  2. Cross-fitting. Always split to avoid overfitting-induced bias.

  3. Modeling choices. Any ML works; in our experiments we used XGBoost with small trees and ridge on the final regression. Hyperparameters aren’t delicate here; the orthogonalization carries a lot of the weight.

  4. Diagnostics. Inspect $\hat b(C)$ (how law changes belt use) and $\hat g(X,C)$ (how belt use changes fatalities given $X,C$); probe SHAP/feature importances to understand heterogeneity.

9) Minimal “how-to” with the code

The repository contains scripts to reproduce the synthetic and FARS analyses. In particular, the supplement references a script named analyze_fars_2000_fd.py for the state seat-belt case study; use it as a template for your own data pipeline.

Generic workflow:

  1. Prepare your data frame with columns $C, X, Z, Y$ (binary $X,Z$ for the current theory).
  2. Choose a learner (FD-DR or FD-R) and ML backends for nuisances ($m,e,q$ or $e_X,m_Z,e_Z,m_Y$).
  3. Enable cross-fitting (2-fold for FD-DR, 3-fold for FD-R) and fit.
  4. Plot $\hat\tau(C)$, summarize by subgroups, and run overlap/weight diagnostics.

(See the repo’s README/examples; keep nuisance models simple and stable—orthogonalization will do its job.)

References

[1] Judea Pearl. Causality: Models, Reasoning, and Inference. 2nd ed., Cambridge University Press, 2009.